概念介紹
在實證研究中探討經濟問題時,常發現問題原因和結果彼此會互相影響,也就是遇到內生性的問題需要解決,例如所得與消費的關係,除了高所得能夠帶動較高的消費金額外,消費多寡的也會對所得有一定程度的影響,因為當人們不消費,將會使廠商獲利縮減, 需要裁員、減薪, 進而影響到所得。
VAR 將所有變數轉為內生變數,發展了結構式VAR 、縮減式VAR 、遞迴式VAR,在此僅討論縮減式VAR 。縮減式VAR解決 了同期資料無法進行預測的問題,利用變數與自身落後期進行迴歸分析。
一般VAR的意義如下面的數學式所表達
$$ y_t = a_1 + b_1x_1 + e_{1t} $$
$$ x_t = a_2 + b_1y_1 + e_{2t} $$
$$ z = [y_t, x_t] $$
$$ z_t = \varphi_1 z_{t-1} + \varphi_2 z_{t-2} + e_t $$
$x$ 和 $y$ 就是兩個會互相影響的變數,所以想辦法把它們兜在一起,合為一個向量,接著用AR模型(在上一章節有提到)進行迴歸分析。
而縮減式VAR的數學表達如下
$$ y_t = \alpha_1 + \varphi_{11} y_{t-1} + \varphi_{12}y_{t-2} + \theta_{11}x_{t-1} + \theta_{12}x_{t-2} + e_{1t} $$
$$ x_t = \alpha_2 + \varphi_{21} y_{t-1} + \varphi_{22}y_{t-2} + \theta_{21}x_{t-1} + \theta_{22}x_{t-2} + e_{2t} $$
有了自身落後期的項數能夠進行迴歸, 就能從縮減式VAR來估計結構式中的係數。VAR 在進行分析前和 ARIMA 一樣需要進行定階, 透過訊息準則決定落後的項數。
VAR的分析多用於以下兩類
- Granger Causality 因果關係
- Impulse response 衝擊反應
其中第一類因果關係的分析為諾貝爾經濟學獎得主英國經濟學家Clive Granger在1966年所論證, 故又稱 Granger Causality
我們討論因果關係時,虛無假設常會表示 $x_{t}$ does not Granger Cause $y_{t}$,這裡的 Granger Cause 也能夠解讀為 Predict 的意思,表示 x 對於 y 的預測能力相對不顯著。
至於衝擊反應則是觀察變數產生影響所持續的時間,例如貨幣政策對於經濟的影響、成交量對於股價的影響等等。
範例實作
範例為臺灣自2010年到2019年的失業率(Unemployment)及消費者物價指數(CPI)資料,資料頻率為月頻率。
在學經濟時想必很多人都聽過菲利浦曲線(Phillips Curve) ,紐西蘭的統計學家菲利浦曾在1960年代提出了失業率和通貨膨脹間存在著抵換關係。
我們可這樣來思考,當失業率上升,代表越來越多人失去了工作,意味著失去了收入來源,此時將使得市場上的需求減弱,導致物價下跌,反之亦然,而從通膨的角度來思考,當通貨膨脹增加,表示企業雇用勞工的成本下降,此時將會更有意願招募人力,因此將會使得失業率下降,反之亦然
從兩方面來解讀似乎都有其道理存在,至於兩者間相互影響的關係,就讓我們用模型來進行實作探討,按照慣例先將資料導入
library(readr)
data = read.csv('vector-autoregression.csv')
date = as.POSIXlt(as.Date(data$date))
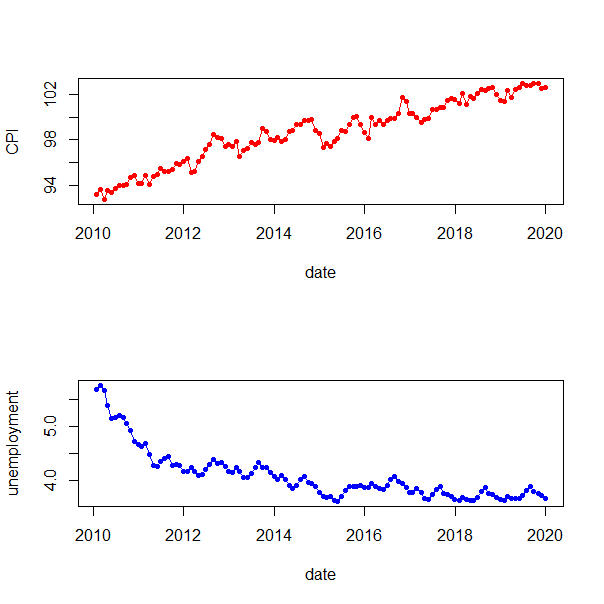
再來試著幫失業率和消費者物價指數繪製走勢圖
dev.new();par(mfrow=(c(2,1)));
plot(date,data$cpi, xlab="date", ylab="CPI",
type='o', col='red',pch=20)
plot(date,data$unemployment, xlab="date", ylab="unemployment",
type='o',col='blue',pch=20)
模型估計
可以看到消費者物價指數是連年的上升,而失業率則是逐年的下降,兩者間看似存在著負向影響的關係,那至於影響持續的情形我們就來透過VAR模型觀察,我們利用SC訊息準則來決定落後階數,可以多試幾種然後比較結果如何,SC傾向資料少,AIC適合資料多
library(vars)
df = data.frame(cpi=data$cpi, unemployment=data$unemployment)
model=VAR(df,ic="sc")
summary(model)
估計結果
印出來的結果洋洋灑灑這麼長一個,我們來把重點擷取出來解讀,往下看
Estimation results for equation cpi:
====================================
cpi = cpi.l1 + unemployment.l1 + const
Estimate Std. Error t value Pr(>|t|)
cpi.l1 0.91899 0.03144 29.229 <2e-16 ***
unemployment.l1 -0.38939 0.18909 -2.059 0.0417 *
const 9.66110 3.75950 2.570 0.0114 *
Estimation results for equation unemployment:
=============================================
unemployment = cpi.l1 + unemployment.l1 + const
Estimate Std. Error t value Pr(>|t|)
cpi.l1 -0.006071 0.004381 -1.386 0.1685
unemployment.l1 0.906806 0.026349 34.415 <2e-16 ***
const 0.963004 0.523859 1.838 0.0686 .
Granger Causality 因果關係
軟體幫忙把等式都寫了出來,而在消費者物價指數作為被解釋變數的等式中,失業率的影響是顯著的,而失業率作為解釋變數後,消費者物價指數的影響反而是不顯著的。 接著我們用Granger Casuality的函式來進行檢定
causality(model, cause = "cpi")$Granger
# Granger causality H0: cpi do not Granger-cause unemployment
#
#data: VAR object model
#F-Test = 1.9203, df1 = 1, df2 = 232, p-value = 0.1672
首先觀察消費者物價指數對失業率的影響,檢定的結果P值為0.1672,相對不顯著,再來我們看看把cause換成失業率會如何
causality(model, cause = "unemployment")$Granger
# Granger causality H0: unemployment do not Granger-cause cpi
#
#data: VAR object model
#F-Test = 4.2405, df1 = 1, df2 = 232, p-value = 0.04059
P值為0.04059,小於0.05,我們認為失業率對消費者物價指數的影響是顯著的。除了一般的檢定外,也可以加上Bootstrap(拔靴法)模擬結果,看看會如何
causality(model, cause = "cpi", boot=TRUE, boot.runs=1000)$Granger
# Granger causality H0: cpi do not Granger-cause unemployment
#
#data: VAR object model
#F-Test = 1.9203, boot.runs = 1000, p-value = 0.143
causality(model, cause = "unemployment", boot=TRUE, boot.runs=1000)$Granger
# Granger causality H0: unemployment do not Granger-cause cpi
#
#data: VAR object model
#F-Test = 4.2405, boot.runs = 1000, p-value = 0.049
cpi為因的P值變小了,但仍然是不顯著,而失業率為因的P值變大,但仍在臨界值內,因此可以解讀作失業率的歷史數據對於消費者物價指數的解釋能力是顯著的
Impulse response 衝擊反應
接著可以透過軟體畫出衝擊反應的圖,觀察衝擊產生後影響持續的時間,利用irf()這個函數,畫出衝擊反應的圖接著來解釋,同時也透過拔靴法模擬,這段程式碼在執行時會需要跑一段時間
ir1=irf(model, impulse = "cpi", response = "unemployment", boot = TRUE,runs=1000, n.ahead = 100)
ir2=irf(model, impulse = "unemployment", response = "cpi", boot = TRUE,runs=1000, n.ahead = 100)
dev.new();plot(ir1)
dev.new();plot(ir2)
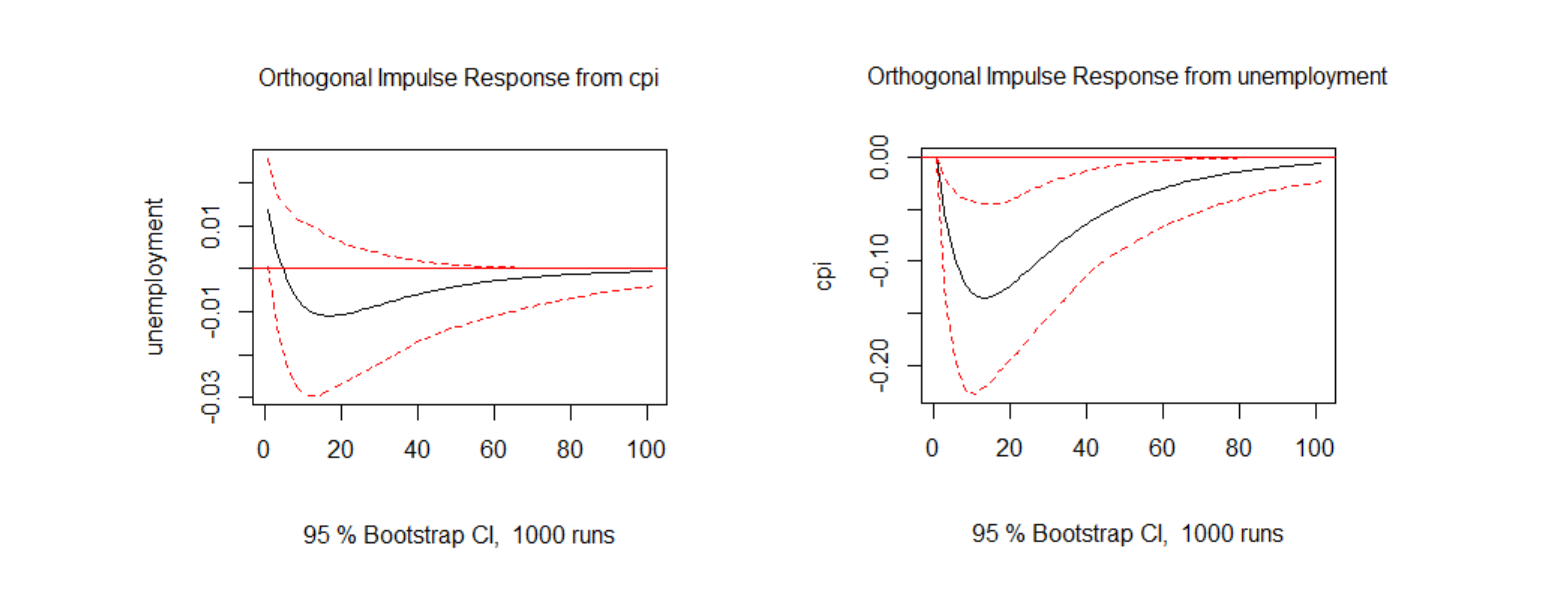
衝擊反應的圖如上面的所示,左邊的為消費者物價指數對於失業率的衝擊,而右邊的則為失業率對於消費者物價指數的衝擊,至於要如何解釋呢?
- 可以發現到消費者物價指數對於失業率的衝擊幅度較小,持續時間也較短
- 右邊的圖可以明顯發現到失業率衝擊帶來的影響一直到40期都還有明顯的影響存在
- 而搭配上面Granger Casuality的結果,專注在右圖,認為失業率對消費者物價指數帶來的衝擊影響較為明顯且持續時間較長
後記
VAR模型能夠幫助我們解決內生性的問題,較不用擔心找了解釋變數和被解釋變數之間如果有因果關係的話,導致不知道如何研究,是個好學習也實用的模型呦。
參考資料
Basic Time-Series Analysis: The VAR Model Explained
16.1 Vector Autoregressions | Introduction to Econometrics with R
R tutorials, R plots, plot(), plot function, plot function and parameters

