資產訂價
所謂的資產訂價就是利用數學模型計算金融商品價格的動作,資產訂價一直是個令人著迷的議題,透過模型搭配參數計算價格,捕捉金融商品的價格變化,除了交易本身的魅力外,背後帶來的利潤也是原因之一,金融市場中大量運用數學最著名的例子就是文藝復興,而他們的出名和低調,也為財務工程增添了不少神秘的色彩。
在臺灣眾多的衍生性金融商品當中,台指選擇權一直以來穩坐期交所交易量的第一名。
主要的原因有幾個,像是因為標的資產為台灣加權股價指數的關係,台指選能夠更直接反映市況,讓投資人可以有感參與市場,再來1點50元的權利金,也降低了參與投資的門檻…等
本篇將透過Python實做兩個基礎的選擇權評價模型-Black-Scholes和二元樹來對台指選擇權價格進行評價,看看效果如何。
Black-Scholes Model
其實 Python 在實作一般的評價模型上並不會特別困難,主要原因就是最困難的部份(提出模型)已經有人完成了,我們需要做的是理解和使用。
$$ d_1 = \frac{ln\frac{S}{K} + (r+\frac{\sigma^{2}}{2})T}{\sigma\sqrt{T}} $$
$$ d_2 = \frac{ln\frac{S}{K} + (r-\frac{\sigma^{2}}{2})T}{\sigma\sqrt{T}}=d_1 - \sigma\sqrt{T} $$
模型中假設股價報酬率為對數常態分配(Lognormal distribution) ,而至於在計算 call 和 put 中使用到的 $N(d_1)$ 和 $N(d_2)$,皆為累積機率密度函數,代表意義根據 John Hull 的財工聖經中是這麼解釋的
$$ c = S_0N(d_1) - Ke^{-rT}N(d_2) $$
$$ p = Ke^{-rT}N(-d_2) - S_0N(-d_1) $$
- $N(d_1)$ 為在風險中立的世界中,資產價格不低於K的機率
- $N(d_2)$ 為執行選擇權的機率
更多的細節推導可以參考財工的專書,我們來用程式把模型實作出來。
下面是一個已經完成的 Black-Scholes 的function,所需要給定的參數就如同平常看到的B-S Model無異
Black-Scholes Model 程式碼
def black_scholes_pricing_model(
option_type: str,
s: float,
k: float,
r: float,
v: float,
q: float,
t: float
) -> float:
"""
Parameters:
option: option type, use 'call' or 'put'
s: spot price
k: strike price
r: interest rate
v: volatility
q: yield rate
t: maturity(year)
"""
d1 = (np.log(s / k) + (r - q + v**2 / 2) * t) / (v * t**0.5)
d2 = d1 - v * t**0.5
call = s * st.norm.cdf(d1) - k * np.exp(-r * t) * st.norm.cdf(d2)
put = k * np.exp(-r * t) * st.norm.cdf(-d2) - s * st.norm.cdf(-d1)
if option_type == "call":
return max(call, 0)
elif option_type == "put":
return max(put, 0)
else:
raise ValueError("Wrong option input.")
二元樹(Binomial Tree)
在二元樹模型中,每個節點(node)的股價都會有兩個結果,上升(up)或下降(down),如同模型名稱般,結果為 Binary 的形式。
從這樣的表示方式也能明顯感受出二元樹相對 B-S Model 來得淺顯好懂許多。
在使用模型時,會設定要將現在(now)至到期日(maturity)間切分為多少節點($n$),例如預估半年後到期的選擇權,$T=6/12=1/2$,而切成10期的話,每期時間變動將會是 $0.5/10 =0.05$,也就是公式中的 $\Delta t$。
而每個節點上升和下降的幅度計算如下
$$ u = e^{\sigma \sqrt{\Delta t}} d = e^{-\sigma \sqrt{\Delta t}} $$
$\Delta t$ 即為每期的時間變動,利用資產價格的波動度呈上微小時間變動,計算出每個節點可能出現的上升和下降價格。
至於每個節點上升和下降機率,計算公式如下
$$ P^{*} = \frac{e^{\mu \Delta t} - d}{u-d} $$
如同 B-S Model 和許多的財務模型,二元樹模型也是假設投資人為風險中立的情況,因為這樣的假設也代表風險增加的情況下,投資人不要求更高的預期報酬。
John Hull 的財工聖經中寫到兩點為何許多模型都以風險中立假設
- 對於資產價格的預期報酬率能以無風險利率表示
- 資產價格也就能用無風險利率進行折現
有了預期價格和機率,也就能夠算出期望值,每一期的資產價格參考下圖
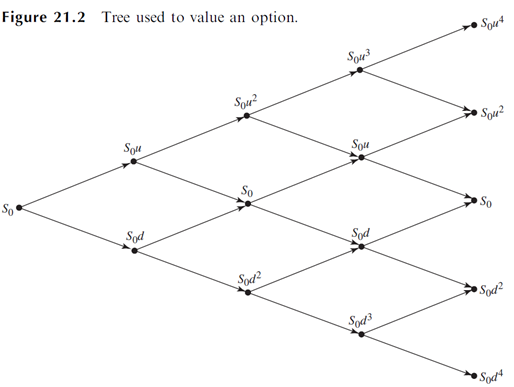
假設總共有N期,第N期中各節點的選擇權價格,以代數表示可以寫成
$$ f_{N,j}=max(S_0u^{j}d^{N-j}-K, 0), j=0,1,...N $$
這是 call 的計算,如果 put 的話便是把資產價格和執行價格對調即可,而每一節點選擇權價格相當於下一期上升和下降價格取期望值後折現。
$$ f_{i, j} = e^{-r\Delta t}[pf_{t+1, j+1}+(1-p)f_{i+1, j}]] $$
簡單來說,用二元樹評價用法就是
- 先算出到期日各個節點的選擇權價格
- 再用到期日的價格回推當前的選擇權價格
台指選是屬於歐式選擇權,和美式選擇權最大不同在於無法提前履約。
也因此程式中就沒刻意計算各節點中的預期資產價格,不然評價美式選擇權的工序其實又更多了。
如果寫成程式就像這樣(直接寫歐式其實比較偷懶些 😆),和B-S模型需要的參數幾乎相同,唯獨多了一樣期數($n$)。
二元樹(Binary Tree)程式碼
import scipy.stats as st
import numpy as np
def binomial_tree_pricing_model(
option_type: str,
s: float,
k: float,
r: float,
v: float,
q: float,
t: float,
n: int,
) -> float:
"""
Parameters:
option_type: option type, use 'call' or 'put'
s: spot price
k: strike price
r: interest rate
v: volatility
q: yield rate
t: maturity(year)
n: periods
"""
delta_t = t / n
u = np.exp(v * np.sqrt(delta_t))
d = np.exp(-v * np.sqrt(delta_t))
p = (np.exp((r - q) * delta_t) - d) / (u - d)
asset_price = [s * (u**j) * (d ** (n - j)) for j in range(n + 1)]
if option_type == "call":
option_price = [max(s - k, 0) for s in asset_price]
elif option_type == "put":
option_price = [max(k - s, 0) for s in asset_price]
else:
raise ValueError("Wrong option input.")
option_tree = [[] for _ in range(n)]
option_tree.append(option_price)
for i in range(1, n + 1):
last_level = option_tree[n - i + 1]
for j in range(1, len(last_level)):
down_price = last_level[j - 1]
up_price = last_level[j]
option_tree[n - i].append(
np.exp(-r * delta_t) * (up_price * p + down_price * (1 - p))
)
return option_tree[0][0]
台指選擇權評價
接著用模型來對選擇權進行評價,使用的資料為 2021/5/24 臺指選 16600 的 Call 和加權指數,資料頻率皆為 1 分鐘。
即便選擇權開盤時間為 8:45 至 13:45,但我們還是配合大盤開盤時間從 9:00 開始計算,而選擇權資料有些殘缺,但還堪用。
而模型中需要的波動度,則是用 2001 年 2 月至今的加權指數日資料計算後年化(其實波動度為影響選擇權六大因子中最難估計的),有些更複雜的作法會用預測的波動餵入模型當作參數,我們先用歷史波動度簡化評價作業。
程式碼在讀取資料後,隨即進行價格的估算,模型參數設定如下
s:加權指數每分鐘收盤價
k:16600
r:臺灣銀行三個月定存牌告利率(機動)
v:加權指數歷史波動度
t:到六月的第三個禮拜三前還有22個交易日,故設定 22/252
q:0
n:設定100期(僅二元樹模型須設定)
出來的結果如下圖
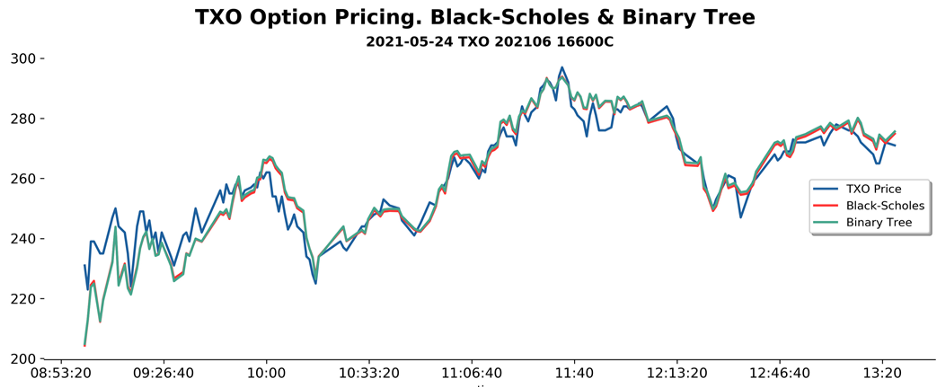
綠色的二元樹和橘紅色的B-S Model兩者的結果幾乎一樣,走勢重疊,令人驚奇的是代入了日內的加權指數價格後,在評價上和實際價格的吻合度好高 。
我也嘗試用過同樣的方法計算週選,結果並不是很理想,週選的波動度應該是大上許多,用長期計算的數據跑出來的評價都普遍偏低。
但沒想到月選的結果會如此貼合,不過畢竟這邊示範的月選資料只有一天,要下結論需要更多的資料驗證。
參考資料
Options, Futures, and Other Derivatives, Global Edition(English and Spanish Edition)

