什麼是風險?
風險就是資產預期減損的幅度或數額。當投資標的走勢和預期相左,預產產生虧損的數額即為風險。
在財金的世界裡,有幾個著名衡量風險的指標,也是本篇介紹的主題,分別為波動度、風險值、條件風險值,
波動度(Volatility)
在財金領域中,波動度是最為普遍用於衡量資產風險的指標,其計算方式即為統計學中的標準差(standard deviation),公式如下
$$\sigma = \sqrt{ \frac{\sum_{i=1}^n{(x_i- \bar{x})^2}}{n-1}}$$
當一資產波動度越高,則認為風險越大,通常會計算資產過去一段時間報酬率的波動度,藉以衡量該資產的風險。
如同前面所述,所謂的風險即為資產價格的變動。
風險值(Value at risk)
在財務世界中,風險的意思即為資產減損的幅度或數額,對於投資人來講,投資產生的虧損即為風險,而風險又能依原因細分許多類型,例如市場風險(Market Risk)、信用風險(Credit Risk)…等等。
風險值(Value at Risk, VaR)是用於判斷投資組合可能產生風險的指標,依Johu Hull財工聖經中寫道
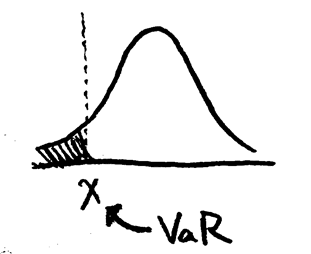
在 α%信心水準下,預期未來 N 天內投資組合可能發生的損失不會超過 X,此X,即為 VaR
如同上方的示意圖,假如左方塗滿的區塊為5%,則X即為95%信心水準下的風險值。
計算的公式如下,由資產平均報酬 加上 波動度乘上信心水準隱含的z分數
$$VaR = \mu + \sigma \times Z(\alpha)$$
而以上僅是一天的風險值,如果要預測 N 天內呢? 即乘上N開根號,相當於一般年化的概念。
而以上僅是一天的風險值,如果要預測 N 天內呢? 即乘上N開根號,類似於年化的概念。
$$VaR \times \sqrt{N}$$
舉例而言:如果投資組合資產價值平均為200萬,標準差為500,則未來1天 95%信心水準下的VaR為多少?
$$200-500\times1.645=-622.5$$
如果10天期則為
$$-622.5\times \sqrt{10}=-1,698.52$$
條件風險值(Conditional VaR, CVaR/Expected Shortfall, ES)
即便用了VaR來預估預期損失,但在預估是假設資產波動呈現常態分佈,然而為了因應**厚尾(fat tail)**的情況,也就有Expected Shotfall的誕生,或者有另一個常聽到的名稱為 Conditional VaR。
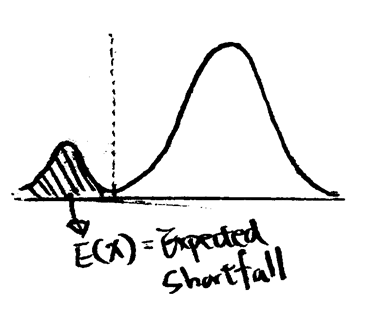
ES的概念其實很好理解,在給定的信心水準(confidence level)和一段期間(T)下,去計算可能產生的預期損失。
從上面的示意圖可以發現,其實在尾端未必如常態分佈機率逐漸減少,而是可能又有一個峰的存在,而ES就是要算出尾端風險的期望值。
在John Hull的風險管理書中用這兩句話來分別解釋VaR和ES,簡單又好懂
"How bad can things get?" -> VaR "If things do get bad, what is the expected loss? -> ES
至於計算公式如下,從ES右方的公式也能看出假設可能產生損失的區塊亦為一常態分配。
$$ES = \mu + \sigma \frac{e^{-Y^{2}/2}}{\sqrt{(2\pi)}(1-X)}$$
公式中的 Y 和 X 關係可以理解為,Y 為在標準常態分佈下,(1-X)% 信心水準下的臨界值,舉例而言,X為1%,則為即為99%信心水準的臨界值,即為-2.326。

