超額報酬 & 系統風險
在投資領域中,大家或許都聽過超額報酬(Risk Premium)或是系統風險(Systemic risk)這兩個專有名詞,而其代表的意思為何呢?
這要從投資學理論中最廣為流傳的評價模型 — 資本資產定價模型(Capital Asset Pricing Model, CAPM) 說起,早期學者們認為能投資組合在被完全多角化分散後,公司個別風險會因為完全多角化的關係降低到幾乎可以忽略,只能透過承擔更多的系統風險來獲得高額報酬
令大盤指數為解釋變數,個股為被解釋變數, 迴歸後得到的估計係數即當作系統風險。
數學表達如下
$$ E(R_i) = \alpha + \beta E(R_m) + \epsilon_i $$
起初稱作單因子模型(Single index model),而後加上了無風險利率,模型變成
$$ E(R_i) - R_f = \alpha + \beta [E(R_m) - R_f] + \epsilon_i $$
也就是廣為人知的CAPM,而在這出現的Alpha和Beta即為文章開頭所指的兩個專有名詞
而其中的 $\alpha$ 即為超額報酬,$\beta$ 為系統風險
當Alpha顯著大於0時,表示股價被低估,高於期望值,反之亦然。而Beta的部份則可以觀察上面的模型公式,發現到如果大盤報酬率為正,Beta愈大,個股預期報酬率將越高
接著將用Python來進行實作,我們利用加權股價指數作為解釋變數,運用迴歸分析來計算台灣50(0050)成份股的Alpha和Beta,用的是調整後股價,也就是有包含股利,不扣股息的價格。
利用CAPM模型估計台灣前五十大成份股
按照慣例,我們先讀取資料,並看一下部份資料
import pandas as pd
price_df = pd.read_csv(
'price_data.csv', index_col='Date', parse_dates=['Date']
)
price_df.head()
接著就直接來做迴歸分析,估計係數,因為使用調整過後的股價,所以大盤指數也用包含股息的報酬指數替代原來的加權股價指數。
我們把每先把報酬率計算出來,存成 return_df ,再把每次迴歸估計的係數存進對應的list中
import statsmodels.api as sm
return_df = price_df.pct_change()
final_output = {}
alpha_list = []
beta_list = []
ERI = []
for company in return_df.columns[2:]:
data_df = pd.concat([return_df[company], return_df['報酬指數']], axis=1).dropna(axis=0)
data_df.columns = [company, 'index']
X = data_df[['index']].assign(Intercept=1)
Y = data_df[company]
X1 = sm.add_constant(X)
model = sm.OLS(Y, X1)
results = model.fit()
alpha = pd.read_html(
results.summary().as_html(), header=0, index_col=0
)[1].iloc[1][0]
beta = pd.read_html(
results.summary().as_html(), header=0, index_col=0
)[1].iloc[0][0]
ERi = (alpha + beta*return_df['報酬指數'].mean())*252
final_output[company] = [alpha, beta, ERi]
alpha_list.append(alpha)
beta_list.append(beta)
ERI.append(ERi)
證券市場線(Security Market Line, SML)
估計後,我們再把結果畫成圖,並在每個股票旁邊標記名稱,並標出證券市場線(Security Market Line, SML),X軸為系統風險,Y軸為對應的報酬率。
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import numpy as np
font_pro = FontProperties(fname='C:\\Windows\\Fonts\\mingliu.ttc')
fig, ax = plt.subplots(figsize=(10, 6))
fig.suptitle('Single Index Model — Taiwan 50 Components', fontsize=20, fontweight='bold')
fig.subplots_adjust(top=0.88)
ax.set_title('2017/12/01–2020/11/30', fontsize=14)
ax.scatter(beta_list, ERI, c='#047cbd')
for k, v in final_output.items():
ax.annotate(k, (float(v[1]), float(v[-1])), fontproperties=font_pro)
ax.axhline(y=0, color='k', ls='-', alpha=0.5)
ax.axvline(x=0, color='k', ls='-', alpha=0.5)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
x1, x2 = 0, 2
y1, y2 = 0, return_df['報酬指數'].mean()*252*2
plt.xticks(np.arange(-0.4, 2.1, 0.4))
plt.plot([x1, x2], [y1, y2], 'k--', linewidth=2)
plt.show()
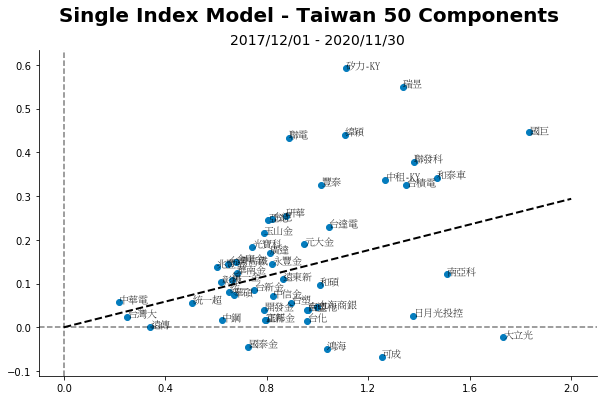
在證券市場線能想作其系統風險對應的報酬率,而在證券市場線之上代表股票表現高於預期報酬率,相對地證券市場線之下股價表現低於預期報酬率。
投資人將會買進證券市場線上方的股票,因為更高的預期報酬,另一層面也代表著股價受到市場低估。
迴歸結果視覺化
接著我們也來看看個股個估計結果,下方的程式碼以台積電(2330.TW)為例,換成其他股票只需要代換股票代號即可。
data_df = pd.concat(
[return_df['台積電'], return_df['報酬指數']], axis=1
).dropna(axis=0)
data_df.columns = [company, 'index']
X = data_df['index']
Y = data_df[company]
X1 = sm.add_constant(X)
model = sm.OLS(Y, X1)
results = model.fit()
alpha = round(
pd.read_html(results.summary().as_html(), header=0, index_col=0
)[1].iloc[0][0], 4
)
beta = round(
pd.read_html(results.summary().as_html(), header=0, index_col=0
)[1].iloc[1][0], 4
)
fig, ax = plt.subplots(figsize=(10, 6))
fig.suptitle(
'Taiwan Semiconductor Manufacturing Co., Ltd.(2330.TW)',
fontsize=20,
fontweight='bold'
)
fig.subplots_adjust(top=0.88)
ax.set_title('alpha={}, beta={}'.format(alpha, beta), fontsize=14)
ax.scatter(X, Y, alpha=0.5, color='orchid')
y_pred = results.predict(X1)
ax.plot(X, y_pred, '-', color='darkorchid', linewidth=2)
ax.axhline(y=0, color='k', ls='-', alpha=0.5)
ax.axvline(x=0, color='k', ls='-', alpha=0.5)
plt.xticks(np.arange(-0.10, 0.11, 0.02))
plt.yticks(np.arange(-0.10, 0.11, 0.02))
fig.show()
輸出結果
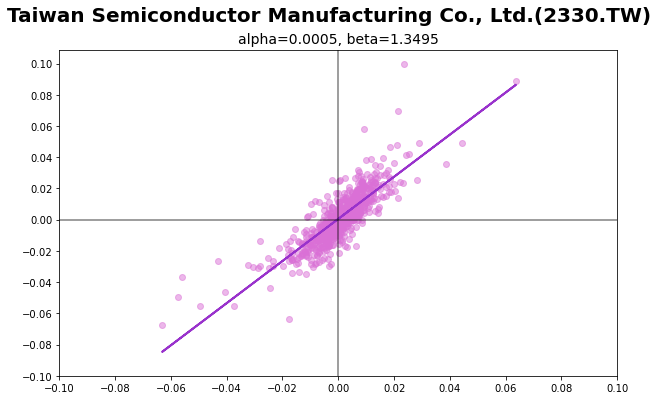
以下分別為四檔股票的估計結果視覺化,可以看到各檔股票的斜率都不太相同,這邊特別挑出了四檔不同類型的股票作比較
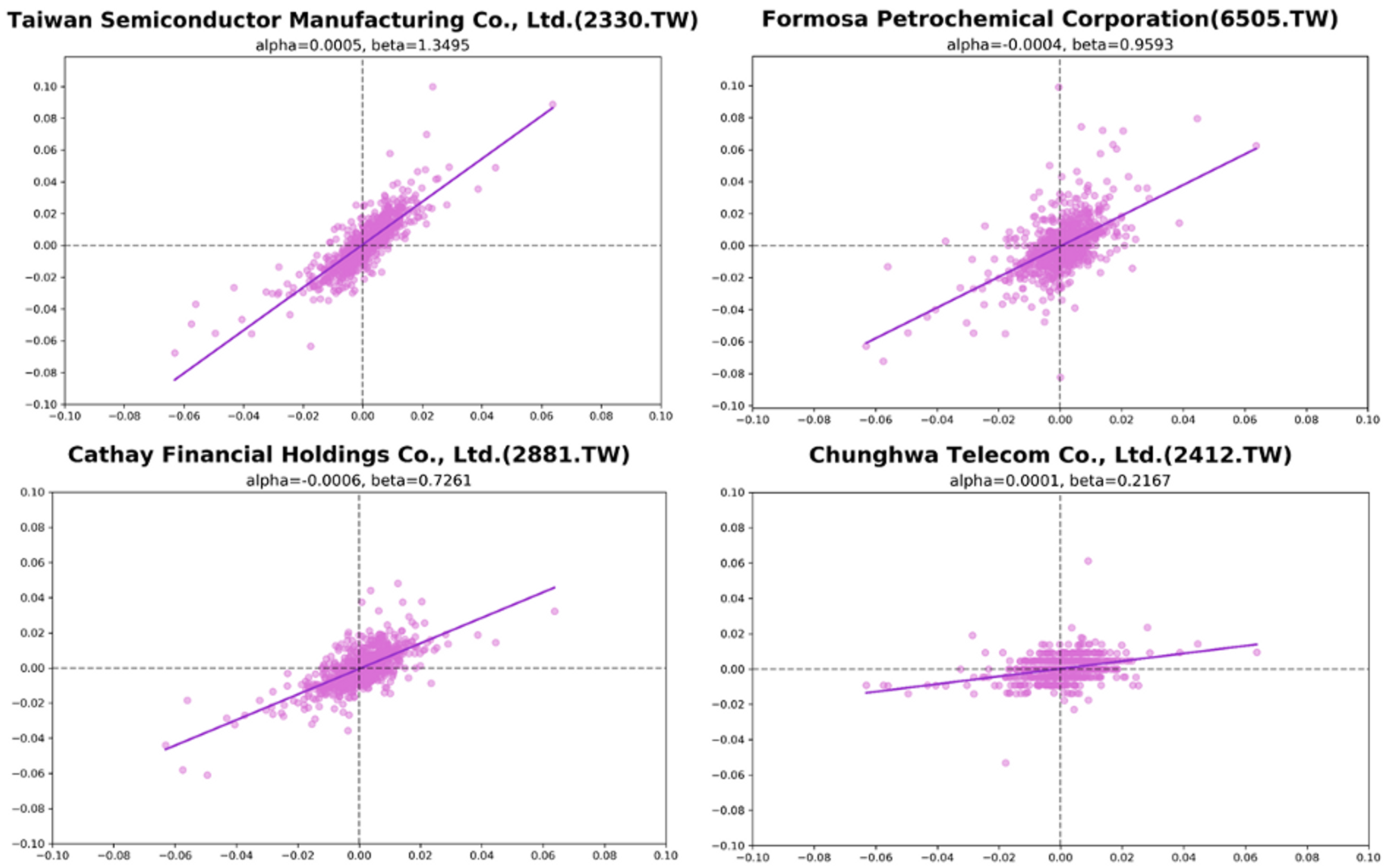
像在最左上角的即為台積電(2330.TW) ,估計出的Beta為1.35,Beta大於1,屬於積極型的股票。 而右上角為台塑化(6505.TW) ,傳產股票的波動相對較為平穩,而台塑化估計出的係數為0.96,股價走勢幾乎和大盤相似。
左下角則為 國泰金(2881.TW),估計出來係數為0.72,相對於半導體和傳產股票,金融股投資人穩健保守許多,股價和大盤的連動性也就更低了些。
右下角則為存股投資人喜好的中華電(2412.TW),受到青睞其中一個原因也是因為股價非常牛皮,從估計結果為0.22也能看出來,中華電股價鮮少受到市場波動的影響。
最終的估計結果則是發現
- 只有很少數的Alpha能夠顯著,50檔股票其中P值小於10%僅有3檔
- Alpha即便是顯著也相當微小
- Beta的部份幾乎都呈現顯著,可以解釋個股的報酬率被市場報酬率影響
以上就是今天的分享,學習了財務金融中相當著名的資本資產訂價模型,利用市場報酬率解釋股票報酬率。

