- 關於報酬率
- 算數平均數(Arithmetic mean)
- 算術平均數的缺陷
- 年化報酬率/幾何平均數(Annualized Return/ Geometric mean)
- 內部報酬率(Internal Rate of Return, IRR)-考慮時間價值
- Excel - XIRR函數
關於報酬率
報酬(Return)和風險(Risk)是財務金融界不斷被探討的主題,因為在財金領域中,和投資相關的計算,即便計算過程再為繁瑣,最終多數仍是為了闡述報酬和風險的概念。
所謂的報酬率,廣泛的定義為投資獲利佔投入本金的比例,例如對一檔投資標的投入 10 萬元本金,在獲利了結後有 2 萬元的淨獲利,則報酬率為 2/10=20%
有投資理財的人多數也有記帳的習慣,但該如何衡量自己的投資報酬率呢? 本篇將介紹三個常見的報酬率計算方法。
算數平均數(Arithmetic mean)
算數平均數為最常見,也是大眾最為理解的報酬率計算方法。
舉例而言,假設投資人在T年投資了 50 萬元購買台積電的股票,而五年過後,持有股票的價值上漲到 80 萬元,獲利為 30 萬元,總報酬率即為
$$ \frac{(80-50)}{50} = 0.6 = 60% $$
算術平均數即為總報酬率除以投資期間
$$ \frac{60%}{5} = 12% $$
當利用算術平均數計算投資報酬率時,可以說這筆投資在過去五年,每年的報酬率有 12%。
現在反過來用 12% 模擬投資部位的變化,看看計算結果如何。持有股票的價值用下方的公式計算。
$$ 部位價值_t = 部位價值_{t-1} *(1+報酬率_t) $$
計算結果
| 年份 | 報酬率 | 部位價值 |
|---|---|---|
| 0 | 0 | 500,000 |
| 1 | 0.12 | 560,000 |
| 2 | 0.12 | 627,200 |
| 3 | 0.12 | 702,464 |
| 4 | 0.12 | 786,760 |
| 5 | 0.12 | 881,171 |
投入本金 50 萬,每年 12% 的報酬率,在五年過後的價值變為 88 萬多,為何會跟原本舉例的 80 萬不同呢? 從這便能發現算術平均數存在著缺陷。
為何會這樣呢?
算術平均數的缺陷
算數平均是大眾最為理解的報酬率計算方法,但透過前面的例子就知道算術平均數存在著缺陷。
造成缺陷最大的原因就是,算術平均數沒有考慮到價值增加部份所產生的報酬率
延續上面的例子來看,這次新增一個價值增加的欄位
| 年份 | 報酬率 | 部位價值 | 價值增加 |
|---|---|---|---|
| 0 | 0 | 500,000 | |
| 1 | 0.12 | 560,000 | 60,000 |
| 2 | 0.12 | 627,200 | 127,200 |
| 3 | 0.12 | 702,464 | 202,464 |
| 4 | 0.12 | 786,760 | 286,760 |
| 5 | 0.12 | 881,171 | 381,171 |
實際上每一期的部位價值,除了原本投入本金帶來的報酬率外,增值的部份也會產生報酬。
每一期的部位價值計算應為
$$ 部位價值_t = (價值增加_{t-1} + 投入本金 )*(1+報酬率_t) $$
以年份2為例,可以寫作
$$ 627,200 = (60,000+500,000)*(1+12%) $$
算術平均數未考量到投資獲利的再投入,因此在計算上容易有高估的情況,投資獲利並非單純由本金所產生,也包含了部份的投資獲利再投入。
年化報酬率/幾何平均數(Annualized Return/ Geometric mean)
即便算術平均數擁有好理解的特性,仍然有其缺陷存在,接著介紹的年化報酬率,便解決了這個問題
年化報酬率就是考量了獲利再投入的報酬率,如果從書本上看到,通常寫作幾何報酬率
延續上節的例子,假設投資人在T年投資了 50 萬元購買台積電的股票,而五年過後,持有股票的價值上漲到 80 萬元,獲利為 30 萬元,總報酬率即為
$$ \frac{(80-50)}{50} = 0.6 $$
年化報酬率計算的公式為
$$ (1+總報酬率)^{\frac{1}{年份}} -1 $$
套到例子,年化報酬率計算為abc
$$ (1+0.6)^{\frac{1}{5}}-1 = 0.09856 $$
而年化報酬率的公式其實不難理解,期末的部位價值即為期初本金每年不斷複利的結果,期末部位價值為 80 萬,期初為 50 萬
寫成公式如下
$$ 500,000*(1+r)^{5} = 800,000 $$
求報酬率的過程為
$$ (1+r)^{5} = \frac{800,000}{500,000} $$
$$ 1+r = 1.6^{\frac{1}{5}} $$
$$ r = 1.6^{\frac{1}{5}} -1 $$
$$ r = 0.09856 $$
由此可知,上方年化報酬率公式為複利過程演變而來的。
這時再驗算一下,把報酬率代回去計算,看到下方表格的結果,這次求得的報酬率,就包含了部位增值的再投資,報酬率為 9.856% ,明顯低於算術平均數的 12%。
因此當利用年化報酬率計算投資報酬率時,可以說這筆投資在過去五年,每年的報酬率約為 9.856%。
| 年份 | 報酬率 | 部位價值 |
|---|---|---|
| 0 | 0 | 500,000 |
| 1 | 0.09856 | 549,280 |
| 2 | 0.09856 | 603,417 |
| 3 | 0.09856 | 662,890 |
| 4 | 0.09856 | 728,224 |
| 5 | 0.09856 | 799,998 |
內部報酬率(Internal Rate of Return, IRR)-考慮時間價值
在看完了簡單好懂的算術平均數,和考量了增值部位再投資的年化報酬率後,最後要介紹的是考慮了時間價值的內部報酬率
什麼是時間價值? 時間價值的概念就是貨幣價值會隨著不同時點流入流出而有所不同。
舉例而言,用 1 年的時間賺得 20 萬,和用 10 年的時間獲得賺得 20 萬,很明顯在評論兩者的表現時,會認為只用 1 年時間的投資人表現相對較好。
內部報酬率考量了不同時間點的現金流量,來衡量報酬率。
計算公式如下
$$ \sum_{i=1}^n \frac{C_i}{(1+IRR)^i} = 0 $$
其中
$$ C_i:每期現金流量, IRR:內部報酬率 $$
延續前面的例子,假設投資人在 T 年投資了 50 萬元購買台積電的股票,而五年過後,持有股票的價值上漲到 80 萬元,獲利為 30 萬元,範例中的現金流量表達如下
$$ {-500,000} + \frac{800,000}{(1+IRR)^{5}}=0 $$
此時的計算結果為
$$ {500,000} = \frac{800,000}{(1+IRR)^{5}} $$
$$ (1+IRR)^{5} = \frac{800,000}{500,000} $$
$$ IRR = 1.6^{\frac{1}{5}} -1 $$
$$ IRR = 0.09856 $$
得到的結果和年化報酬率相同。
接著再試看看在第1年底增加投入 10 萬元,期末結果同樣是 80 萬,內部報酬率為多少。
$$ {-500,000} + \frac{-100,000}{(1+IRR)^{1}} +\frac{800,000}{(1+IRR)^{5}}=0 $$
求解後內部報酬率約為 6.127%。
那如果換成第 4 年底投入 10 萬元呢?
$$ {-500,000} + \frac{-100,000}{(1+IRR)^{4}} +\frac{800,000}{(1+IRR)^{5}}=0 $$
求解後內部報酬率約為 6.754%,相比第一年投入 10 萬元的內部報酬率更高,要理解背後的原因其實很直覺。
同樣的獲利下,資金越晚投入,則代表資金發揮的效率更好,這時報酬率理所當然會高些。
Excel - XIRR函數
介紹了內部報酬率後,不得不提記帳的好夥伴 Excel,因為Excel 內建的XIRR函數簡化了計算內部報酬率的困難。
以投資股票為例,很多人都有投資股票的習慣,而除了一開始投入的本金外,有時會因為可用資金增加(加薪、其他收入)而再提高投入本金,此時在準確衡量報酬上就變得更加困難,但XIRR幫助簡化了這件事。
以下圖為例(暫不考慮手續費、交易稅),在 5/16 時投入了 400,000 買入 2 張 200 元的鴻海股票,到 8/6 時獲利了結一張,在 9/12 手上持有一張的股利入帳,而最後的12/25號,就是代表當前的意思,當前手上的股票價值為 20.3 萬。
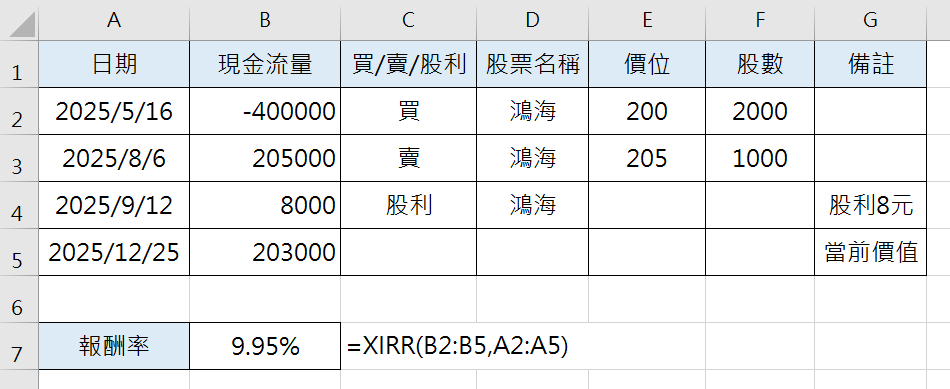
原本在求解上相當困難的算式,透過 C7 儲存格的 XIRR 函數就解決了,求出考慮貨幣時間價值後的報酬率為 9.95%。
投資人不用再特別考慮多少錢準備投入買賣股票,而是考量實際投入的現金流來計算報酬率。
如此一來,在記帳上省力許多,也能更確切瞭解投資的績效。

